Practice 8-2 special right triangles – Practice 8-2: Special Right Triangles delves into the fascinating world of geometry, exploring the unique properties and practical applications of these essential shapes. This comprehensive guide empowers readers with a deep understanding of special right triangles, equipping them with the knowledge and skills to solve complex problems with precision.
Throughout this exploration, we will unravel the intricate relationship between the Pythagorean theorem and special right triangles, uncovering their significance in various fields such as architecture, engineering, and navigation. By mastering the techniques presented in this guide, readers will gain the confidence to tackle real-world challenges involving height, distance, and angles with remarkable accuracy.
Pythagorean Theorem and Special Right Triangles: Practice 8-2 Special Right Triangles
The Pythagorean theorem is a fundamental theorem in geometry that establishes a relationship between the lengths of the sides of a right triangle. It states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Special right triangles are right triangles that have specific side length ratios. These ratios make it possible to calculate the lengths of the sides of the triangle without using the Pythagorean theorem.
Pythagorean Theorem and Special Right Triangles
The Pythagorean theorem can be used to derive the side length ratios of special right triangles. For example, in a 3-4-5 right triangle, the sides have lengths of 3, 4, and 5 units. The Pythagorean theorem can be used to verify that these lengths satisfy the theorem:
32+ 4 2= 5 2
- + 16 = 25
- = 25
Applications of Special Right Triangles
Special right triangles have numerous practical applications in various fields, including architecture, engineering, and navigation. Their unique properties allow for the precise calculation of heights, distances, and angles in real-world scenarios.
Architecture
- Special right triangles are used to determine the height of buildings, towers, and other structures. By measuring the length of the adjacent side and the angle of elevation from a known point, the height can be calculated using the tangent ratio.
- They are also used in designing roofs and windows, where the angles and lengths of the sides must be carefully calculated to ensure proper drainage and ventilation.
Engineering
- In civil engineering, special right triangles are used to calculate the forces acting on bridges, dams, and other structures. By understanding the angles and lengths of the members, engineers can determine the stresses and loads that need to be accounted for.
li>They are also used in mechanical engineering, where they help determine the angles and forces involved in the design of machines and engines.
Navigation
- In navigation, special right triangles are used to calculate the distance between two points, known as the hypotenuse. By measuring the adjacent side and the angle of elevation or depression, navigators can determine the distance to a landmark or the height of a mountain.
- They are also used in celestial navigation, where the angles and distances between stars and the horizon are used to determine the position of a ship or aircraft.
Solving Problems Involving Special Right Triangles
Special right triangles are right triangles with specific angle and side length relationships. They offer efficient solutions to various geometric problems. This guide provides a structured approach to solving problems involving special right triangles, including methods for finding missing side lengths, angles, and areas.
Finding Missing Side Lengths
To find a missing side length, identify the type of special right triangle and use the appropriate formula:
- 30°-60°-90° Triangle:Shorter leg = (1/2) – hypotenuse, Longer leg = (√3/2) – hypotenuse
- 45°-45°-90° Triangle:Legs are equal in length
- 60°-30°-90° Triangle:Shorter leg = (1/2) – hypotenuse, Longer leg = (√3/2) – hypotenuse
Finding Missing Angles
In special right triangles, the angles are fixed:
- 30°-60°-90° Triangle:Angles are 30°, 60°, and 90°
- 45°-45°-90° Triangle:Angles are 45°, 45°, and 90°
- 60°-30°-90° Triangle:Angles are 60°, 30°, and 90°
Finding Missing Areas
To find the area of a special right triangle, use the formula: Area = (1/2) – base – height.
Key Formulas and Identities, Practice 8-2 special right triangles
| Triangle Type | Formulas |
|---|---|
| 30°-60°-90° | shorter leg = (1/2)
|
| 45°-45°-90° | legs are equal in length |
| 60°-30°-90° | shorter leg = (1/2)
|
Geometric Properties of Special Right Triangles
Special right triangles, such as the 30-60-90 triangle and the 45-45-90 triangle, possess unique geometric properties that distinguish them from other types of triangles. These properties stem from the specific relationships between the angles, sides, and altitudes of these triangles.
30-60-90 Triangle
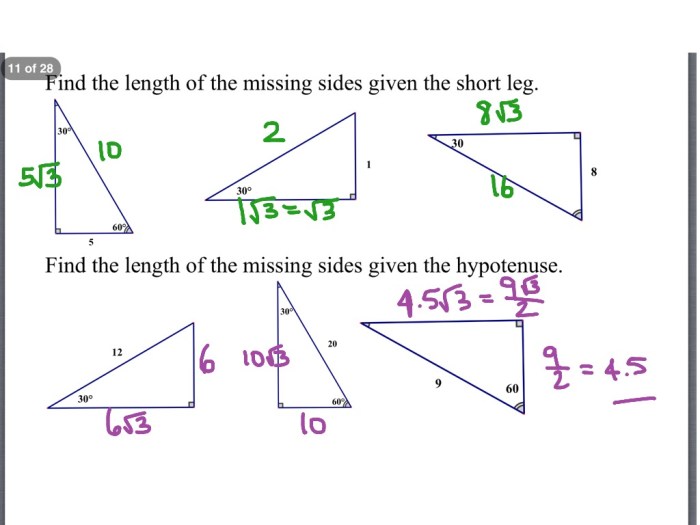
In a 30-60-90 triangle, the angles measure 30°, 60°, and 90°. The side opposite the 30° angle is half the length of the hypotenuse, while the side opposite the 60° angle is √3 times half the length of the hypotenuse.
Additionally, the altitude from the right angle to the hypotenuse divides the hypotenuse into a ratio of 1:√3.
45-45-90 Triangle
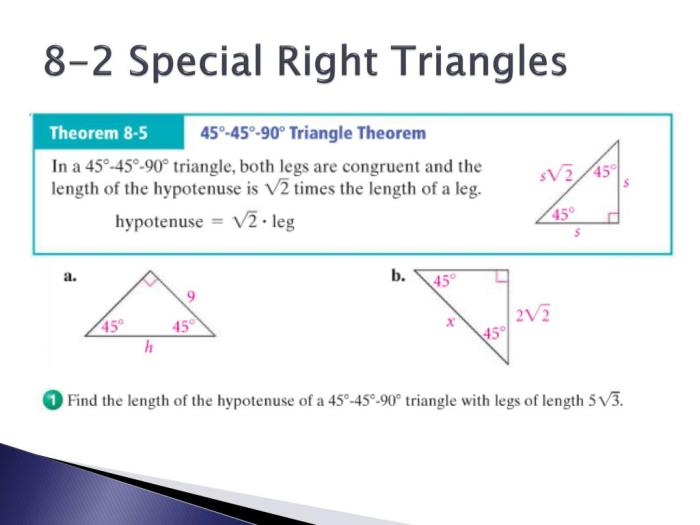
In a 45-45-90 triangle, all three angles measure 45°, 45°, and 90°. The two sides adjacent to the 45° angles are equal in length, and the hypotenuse is √2 times the length of either of these sides. The altitude from the right angle to the hypotenuse bisects the hypotenuse.
FAQ Overview
What are the different types of special right triangles?
There are two main types of special right triangles: the 30-60-90 triangle and the 45-45-90 triangle.
How can I use special right triangles to solve problems?
Special right triangles can be used to solve problems involving height, distance, and angles. For example, you can use the Pythagorean theorem to find the height of a building or the distance between two points.
What are some real-world applications of special right triangles?
Special right triangles are used in a variety of real-world applications, including architecture, engineering, and navigation. For example, architects use special right triangles to design buildings, engineers use them to design bridges, and navigators use them to determine the direction of travel.
